Graphs in Data Structure

Graphs are really just collections of nodes and edges. In the graph, these nodes are often called vertices or vertex for singular, and the connection is often called an edge.

The important thing is here that these nodes can have multiple connections to multiple different nodes.
This is one of the unique characteristics of Graphs, which is where the nodes can have any number of vertices.

💡 Undirected Graphs –

When I say that a graph is undirected, it means that we can traverse from any node to any of its corresponding connected nodes.
This is what happens because these connections are not directed.

💡 Directed Graphs –

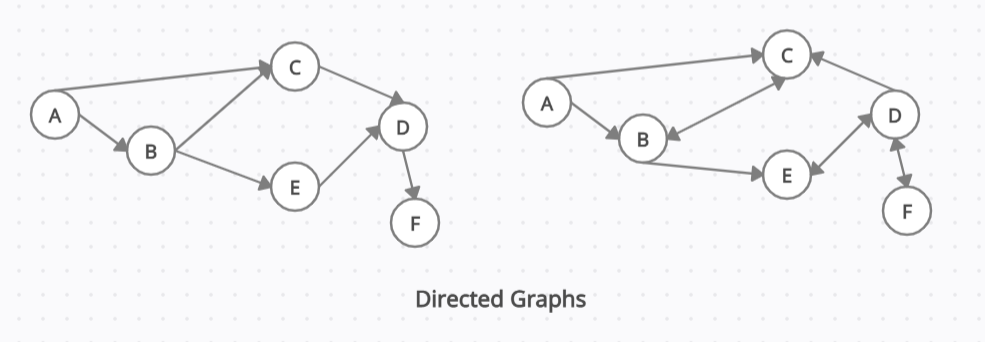
When two nodes of the graph have a direction of traversal with arrow connection then it is called is Directed graph.
Now, these directions don’t necessarily only have to go one way. It’s very possible that a directed graph has arrows that go both ways.

Now, if we picked any two nodes like D and F from the second graph that share a two-directional edge, we’re able to traverse from D to F and F to F as well. This is because the direction of the traversal is no longer limiting us, even though this is a directed graph due to the fact of that two-pointer edge.

💡 Weighted Graphs –

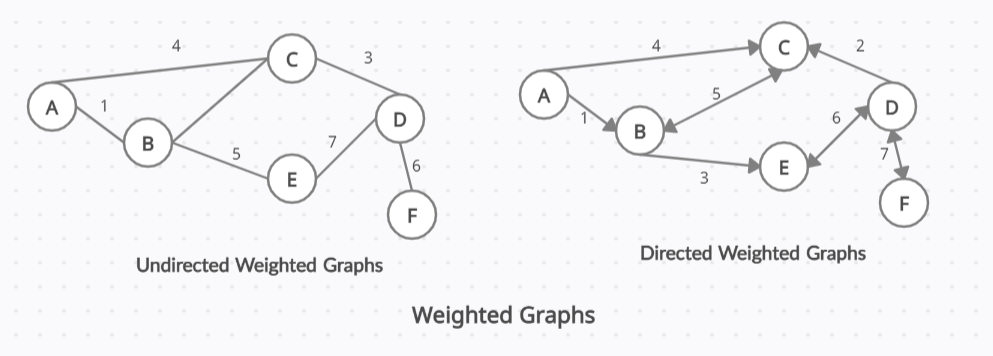
Before this graph, what we have seen was an unweighted graph because there is no cost to traversing across an edge. And this is because these are both unweighted.

So when it is unweighted, it means that there’s no associated weight to any of these edges, whereas a weighted graph does have an associated weight to every edge.

This means that the cost of traversing from one node D to another node F is going to be 6.

In the above Picture If we see the second graph, there is a two-directional edge. This means that regardless of which direction you traverse between these two nodes D & F, you’re going to have to pay that cost of 7. So that’s an important thing to know about these weighted and directed graphs.

💡 Unconnected Graphs –

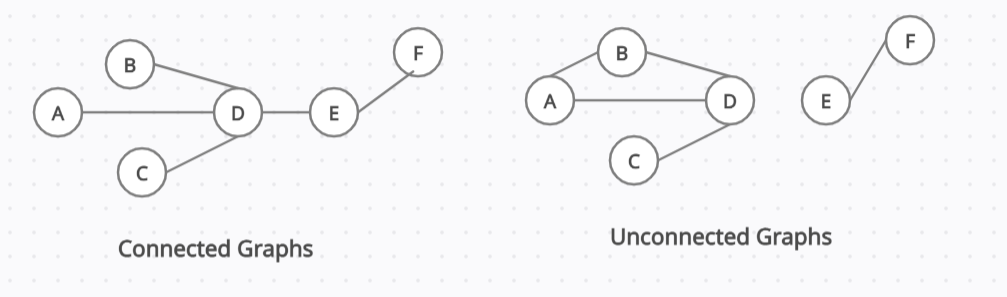
Another variation of the graph that can exist with this format is one where we have different nodes that are connected to other nodes, but the entirety of all the nodes might not be connected as one structure.
So You can see there are almost two different sections that do have connections in their nodes. But these two sections are not joined together.
So when you have this case, this is considered an unconnected graph.

💻 A binary tree is also a graph –

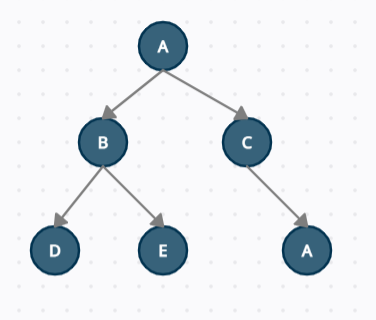
A binary tree is definitely a graph now, all binary trees or graphs, but not all graphs are binary.
Here you can visualize a binary tree as a directed graph that takes the specific shape based on the rules that govern a binary tree.

💻 2 D array is also a graph –

The 2-D array is also considered a graph as well. The reason for this is if you visualize this 2d array as a grid and you visualize every single grid cell value as a vertex, that is connected by a pattern of edges, which represents the traversal pattern that we can make from one cell to another or one edge to another.

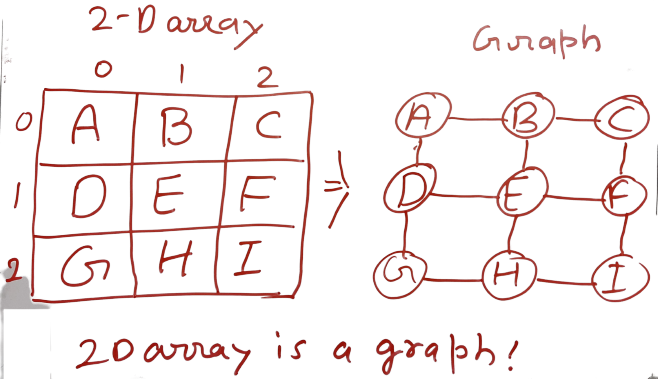
Graphs Adjacency List and Adjacency Matrix –

Now we are going to show you the two most common ways that we can represent our graphs inside of our code, which are the adjacency list and the adjacency matrix.

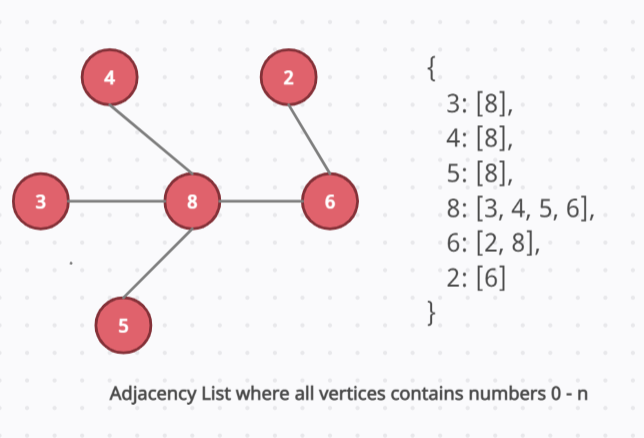
💡 Adjacency List

when I want to represent Graph as an adjacency list, it means I want to represent this graph as an array. The length of this array is the number of nodes present in the graph.
Every index that you see inside of this array points to the corresponding node that has that same number identifier. The value in each of these indexes is going to be an array. And within this array, we’re going to contain the numerical value of any node that is connected to the corresponding node that we’re looking at.

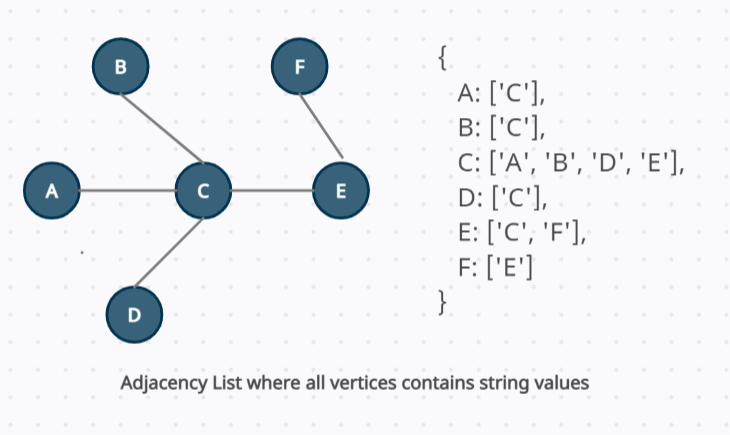
If a graph contains string values, in this case, replace the original array as an object.
If this is the case, the adjacency list is going to take the form of this object where the key is going to be every single node and the value is just going to be an array containing strings that represent the connected vertex notes.

See the below diagram to understand the adjacency List. 👇

💡 Adjacency matrix

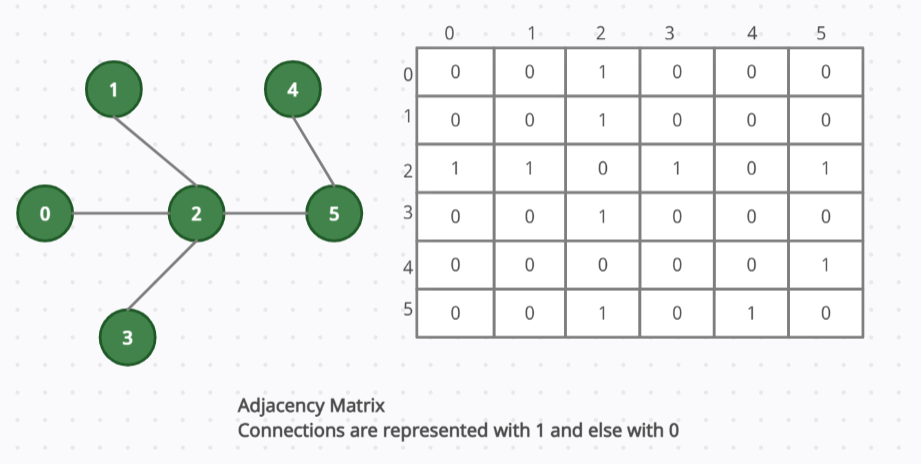
An adjacency matrix is represented as a 2d array. Here we are going to represent each node as the outside arrays, indexes, and then inside for every array, the indices represent, which node is connected to this node that we’re initially looking at.

Graphs in Data Structure

💡 Draw a graph by given an adjacency List

const adjacencyList = [
[1, 3], [0], [3, 8], [0, 2, 4, 5], [3, 6], [3], [4, 7], [6], [2]
];

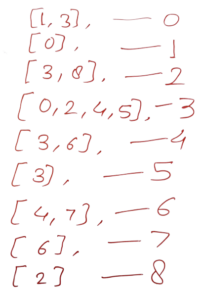
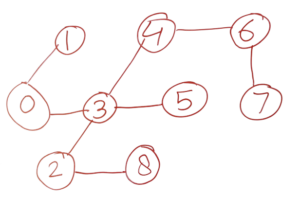
💡 Graph BFS and DFS Algorithms

👇 BFS Traversal

const adjacencyList = [[1, 3], [0], [3, 8], [0, 2, 4, 5], [3, 6], [3], [4, 7], [6], [2]];

• In Simple Questions, we will get either an Adjacency List or a Graph Structure.
• If we get a Graph then we have to convert this in adjacency list or matrix to proceed with our algorithm.
• In most cases, we get a theoretical/logical type question based on some values and we need to draw
• a graph on provided values, logic and then covert that into an adjacency list.

const traversalBFS = (graph) => {
  // BFS uses queue to proceed values and initial start with first element.
  const queue = [0];

  // Here we have taken a seen object. In this we will keep all the visited vertices so that
  // same vertex not visited twice.
  const seen = {};

  // This in an array to keep all traversed element.
  const values = [];

  while (queue.length) {
    const vertex = queue.shift(); // pop first vertex
    values.push(vertex); // push into final array
    seen[vertex] = true; // mark seen true of this vertex

    // Find all connections and visited them
    for (let connection of graph[vertex]) {
      if (!seen[connection]) {
        queue.push(connection);
      }
    }
  }
  return values;
};

*Output*

console.log('traversalBFS(adjacencyList) :', traversalBFS(adjacencyList));

[0, 1, 3, 2, 4, 5, 8, 6, 7]

Graphs in Data Structure

👇 DFS Traversal

const traversalDFS = (graph) => {
  const seen = {}; // keep track of visited vertex
  const values = []; // stored visited vertices

  // called below function 'dfs' recursively
  // 0 - is first vertex that we have chosen to start algorithm.
  dfs(graph, 0, values, seen);

  return values;
};

const dfs = (graph, vertex, values, seen) => {
  values.push(vertex);
  seen[vertex] = true;

  for (let connection of graph[vertex]) {
    if (!seen[connection]) {
      dfs(graph, connection, values, seen);
    }
  }
};

*Output*

console.log('traversalDFS(adjacencyList) :', traversalDFS(adjacencyList));

 [0, 1, 3, 2, 8, 4, 6, 7, 5]

Traversing 2 D array with BFS & DFS Algorithm in JavaScript

Graphs in Data Structure