Traversing 2 D array

💡 First Understand JavaScript multidimensional array

JavaScript does not provide the multidimensional array natively. However, We create a multidimensional array by defining an array of elements, where each element also contains an array.

** 2 D Matrix Example **  
[
  [1, 2, 3, 4, 5],
  [6, 7, 8, 9, 10],
  [11, 12, 13, 14, 15],
  [16, 17, 18, 19, 20],
];

💡 Create 2 D Array in JavaScript

const rows = new Array(4).fill('');
console.log('created blank rows :', rows);

const testBlankMatrix = rows.map(() => new Array(5).fill(false));
console.log('created test matrix of 4 * 5 :', testBlankMatrix);

// Output

 [
  [false, false, false, false, false],
  [false, false, false, false, false],
  [false, false, false, false, false],
  [false, false, false, false, false],
]; 

💡 Let’s See 3-D array Structure – each element of the array is a two-dimensional array.

**  3-D array **

const threeD = [
  [
    [1, 2, 3],
    [4, 5, 6],
  ],
  [
    [7, 8, 9],
    [10, 11, 12],
  ],
];

BFS & DFS

💡 What is BFS?

BFS stands for Breadth-First Search. It is also known as level order traversal.
BFS algorithm uses a queue data structure to track which node to visit next. Upon reaching that element, the algorithm adds it to the queue to visit this later.
When we use the BFS algorithm for the traversal in a graph, we can consider any node as a root node.
BFS is a traversal technique in which all the vertex of the same level are explored first, and then we move to the next level.
BFS does not use the backtracking concept.

A real example of a Queue data structure is waiting in line at the ticket window. Who comes first in line, that will take the ticket first.
Adding an element in the queue is called Enqueue and removing an item from the queue is called Dequeue.

💡 What is DFS?

DFS stands for Depth First Search. In DFS traversal, the stack data structure is used, which works on the LIFO (Last In First Out) principle.
In DFS, traversing can be started from any node, or we can say that any node can be considered as a root node until the root node is not mentioned in the problem.
DFS is also a traversal technique in which traversal is started from the root node and explores the nodes until the node has no unvisited adjacent nodes.
DFS uses backtracking to traverse all the unvisited nodes.

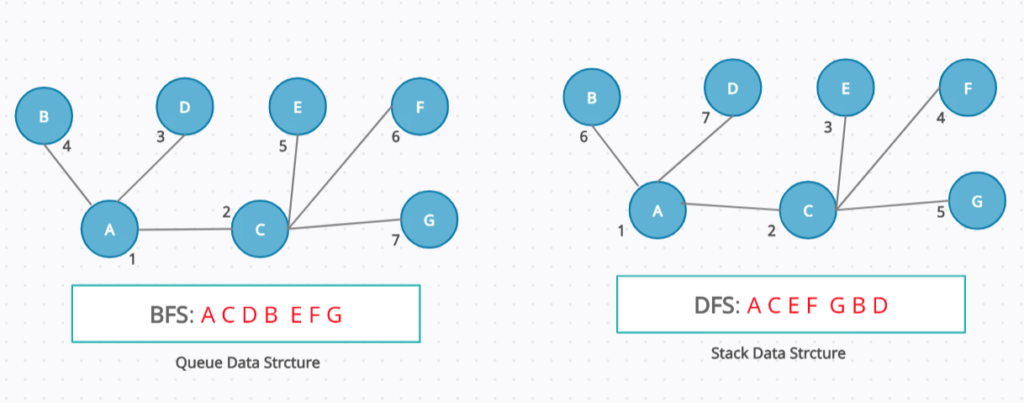
✔ BFS Steps

1. Start from any Node (that is called as root node)
2. Visit that Node and push into Queue
3. Explore all adjacent of visited Node in any order and push all into Queue
4. Once all adjacent pushed into Queue then pick a new vertex
5. This new vertex will be the first non explored element from the queue

✔ DFS Steps

1. Start from any Node (that is called as root node)
2. Visit that Node and push into Stack
3. Explore its adjacent
4. Visit any one of its adjacent and push into Stack
5. Now explore that adjacent
6. Repeat 4 and 5
7. Once there is no adjacent remaining then backtrack to the parent
8. Visit another adjacent of that parent and push into stack
9. If still no any parent’s adjacent then backtrack to its parent.
10. Do this until all vertex traversed.

Learn more differences between BFS & DFS
https://www.javatpoint.com/bfs-vs-dfs

💡 Traversal in 2 D array

Let’s find adjacent of any element in 2 D array

If we see a 2 D array, then we will find that there are 4 adjacent to every element and directions are up, right, bottom, and left.

If we take – (See the first Image of this Post)

Node A - adjacent are ->
up (-1, 0) - undefined
right (0, 1) - B
down (1, 0) -  F
left (0, -1) - undefined

Node H - adjacent are ->
up (-1, 0) - C
right (0, 1) - I
down (1, 0) -  M
left (0, -1) - G

💡 Directions are –

  [-1, 0], //up
  [0, 1], //right
  [1, 0], //down
  [0, -1], //left

Let’s see algorithm of DFS travering in 2 D Matrix

const traversalDFS = (matrix) => {
  if (!matrix.length) {
    return [];
  }

  // store all visited element and finally returned this
  const values = [];

  // created 2-d matrix same as given matrix with falsy values
  const seen = new Array(matrix.length).fill('').map(() => new Array(matrix[0].length).fill(false));

  // call recursive function dfs
  dfs(matrix, 0, 0, values, seen);

  return values;
};

const dfs = (matrix, row, col, values, seen) => {
  // row should not be less then 0
  // row should not be greater then matrix.length
  // col should not be less then 0
  // col should not be greater then matrix.length
  // element should not be visited (seen[row][col])

  const invalidRow = row < 0 || row >= matrix.length;
  const invalidCol = col < 0 || col >= matrix[0].length;
  if (invalidRow || invalidCol || seen[row][col]) {
    return;
  }

  seen[row][col] = true; // marked true so that not to visit this again

  values.push(matrix[row][col]); // push visited element into values array

  for (let dir of directions) {
    dfs(matrix, row + dir[0], col + dir[1], values, seen);
  }
};

** Output **

const testMatrix = [
  [1, 2, 3, 4, 5],
  [6, 7, 8, 9, 10],
  [11, 12, 13, 14, 15],
  [16, 17, 18, 19, 20],
];
console.log('traversalDFS(testMatrix) :', traversalDFS(testMatrix));
> [1, 2, 3, 4, 5, 10, 15, 20, 19, 14, 9, 8, 13, 18, 17, 12, 7, 6, 11, 16]

const test2 = [
  [2, 3],
  [4, 5],
];
console.log('traversalDFS(test2) :', traversalDFS(test2));
> traversalDFS(test2) : (4) [2, 3, 5, 4]

const test3 = [[]];
console.log('traversalDFS(test3) :', traversalDFS(test3));
> traversalDFS(test3) : []

const test4 = [];
console.log('traversalDFS(test4) :', traversalDFS(test4));
> traversalDFS(test4) : []

Let’s see algorithm of BFS travering in 2 D Matrix

const traversalBFS = (matrix) => {
  if (!matrix.length) {
    return [];
  }

  // store all visited element and finally returned this
  const values = [];
  // BFS uses queue to process data, Initially store first element
  const queue = [[0, 0]];

  // created 2-d matrix same as given matrix with falsy values
  const seen = new Array(matrix.length).fill('').map(() => new Array(matrix[0].length).fill(false));

  while (queue.length) {
    const currentPos = queue.shift();
    const row = currentPos[0];
    const col = currentPos[1];

    // row should not be less then 0
    // row should not be greater then matrix.length
    // col should not be less then 0
    // col should not be greater then matrix.length
    // element should not be visited (seen[row][col])

    const invalidRow = row < 0 || row >= matrix.length;
    const invalidCol = col < 0 || col >= matrix[0].length;
    if (invalidRow || invalidCol || seen[row][col]) {
      continue; // continue while loop
    }

    seen[row][col] = true; // marked true so that not to visit this again

    values.push(matrix[row][col]); // push visited element into values array

    // Push adjacent item in to queue
    for (let dir of directions) {
      queue.push([row + dir[0], col + dir[1]]);
    }
  }

  return values;
};

** Output *******

const testMatrix1 = [
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16]
  ];
console.log('traversalBFS(testMatrix1) :', traversalBFS(testMatrix1));
> traversalBFS(testMatrix1) : (16) [1, 2, 5, 3, 6, 9, 4, 7, 10, 13, 8, 11, 14, 12, 15, 16]

const test5 = [
  [2, 3],
  [4, 5],
];
console.log('traversalBFS(test5) :', traversalBFS(test5));
> traversalBFS(test5) : (4) [2, 3, 4, 5]

Traversing 2 D array

+15

-1