LeetCode – Coin Change Problem

Problem LeetCode Link – https://leetcode.com/problems/coin-change/

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

EXAMPLES - 

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Input: coins = [2], amount = 3
Output: -1

Brute Force Solution

var coinChange = function (coins, amount) {
    return minCoins(coins, amount);
};

function minCoins(coinsArr, amount) {
    var requiredCoins = Number.MAX_SAFE_INTEGER;
    if (amount === 0) {
        return 0;
    }
    for (let i = 0; i < coinsArr.length; i++) {
        var remainingAmount = amount - coinsArr[i];
        if (remainingAmount >= 0) {
            var subAns = minCoins(coinsArr, remainingAmount);
        }
        if(subAns >= 0) {
            requiredCoins = Math.min(subAns + 1, requiredCoins);
        }
    }
    if (requiredCoins != Number.MAX_SAFE_INTEGER ) {
        return requiredCoins;
    } else {
        return -1;
    }
}

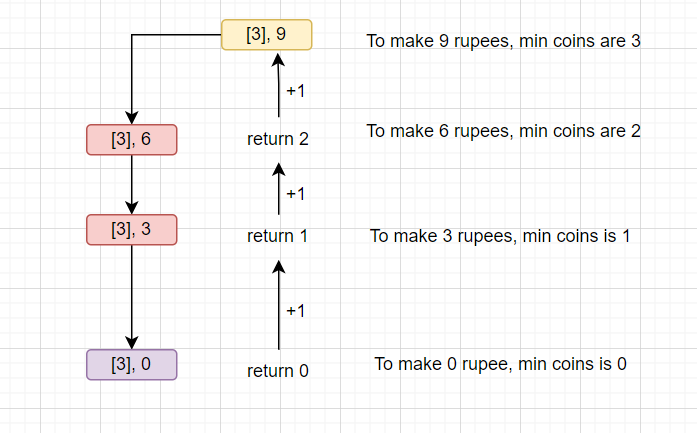
💡 Understand the above solution with the below diagram and find the minimum required coins to make an amount of 9 if we are given a coins array [3].

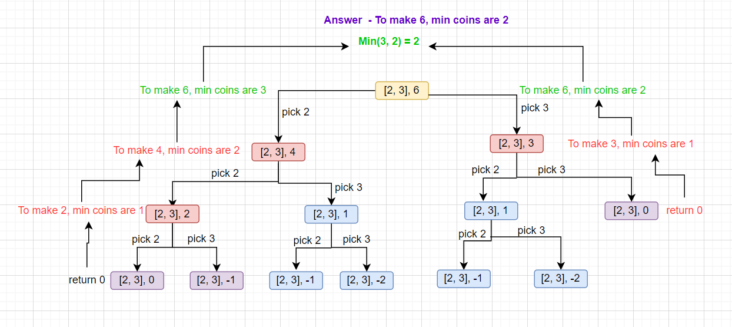
coinChange([2,3], 7); output -> 3
coinChange([2], 3); output -> -1
coinChange([3,8], 54); output -> 8

Let’s try to get the minimum required coins for a big amount like the below

coinChange([186,419,83,408], 6249);

This will run many many times with brute force solution and can give Time Exceed Error. So to solve this, we have to introduce a dynamic programming concept in this solution. And to implement the DP approach, we have to use Memoization technique with this.

Solution with Memoization technique

A dynamic programming approach is used when we have problems that can be divided into similar sub-problems so that their results can be reused. These algorithms are mostly used for optimization.

A dynamic programming technique improves the efficiency of any recursive algorithm that repeatedly solves the same subproblems.

Dynamic programming involves two steps: You find a recursive solution to a problem that has many subproblems that need to be solved.

/**
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function (coins, amount) {
    const dp = [];
    dp[0] = 0;
    return minCoins(coins, amount, dp);
};

function minCoins(coinsArr, amount, dp) {
    var requiredCoins = Number.MAX_SAFE_INTEGER;
    if (amount === 0) {
        return 0;
    }
    for (let i = 0; i < coinsArr.length; i++) {
        let remainingAmount = amount - coinsArr[i];
        if (remainingAmount >= 0) {
            let subAns = 0;
            if (dp[remainingAmount]) {
                subAns = dp[remainingAmount];
            } else {
                subAns = minCoins(coinsArr, remainingAmount, dp)
            }
            if (subAns >= 0) {
                requiredCoins = Math.min(requiredCoins, subAns + 1);
            }
        }
    }
    if (requiredCoins != Number.MAX_SAFE_INTEGER ) {
        dp[amount] = requiredCoins;
    } else {
        dp[amount] = -1;
    }
    return dp[amount];
}

Now run again and we get the answer.

coinChange([186,419,83,408], 6249); output - 20

✔ Array Representation of Binary Tree | Full Tree & Complete Binary Tree

✔ Graphs in Data Structure, Types & Traversal with BFS and DFS, Algorithms

✔ Traversing 2 D array with BFS & DFS Algorithm in JavaScript

✔ JavaScript Rotate 2D matrix 90 degrees clockwise | Top Interview Question

✔ HashTable Data Structure in JavaScript with Add Delete & Search Algorithms

✔ Trie Data Structure – Insert Search Delete & Print Program with JavaScript

✔ Top JavaScript Commonly asked Algorithms in Interview

✔ JavaScript String Permutation Program with nice explanation

LeetCode – Coin Change Problem